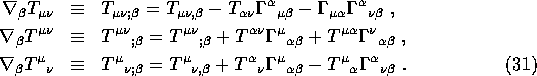is just
since the basis vectors do not vary. In a general spacetime with
arbitrary coordinates, 
with vary from
point to point so
Since 
is itself a vector for
a given 
it can be written as a linear combination of the
bases vectors:
The 
's are called Christoffel symbols [ or the
metric connection ].
Thus we have:
so
Thus we can write
where
Let us now prove that 
are the components of a
1/1 tensor.
Remember in section 3.5 we found that 
was
only a tensor under Poincaré transformations in Minkowski
space with Minkowski coordinates. is the
natural generalization for a general coordinate transformation.
Writing 
, we have:
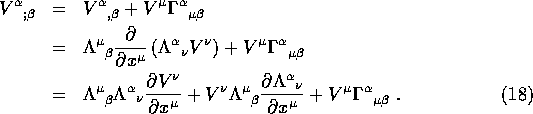
Now
therefore
so we obtain:
Now using 
, 
and 
we obtain:
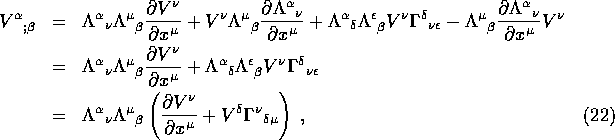
so
We have shown that are indeed the components
of a 1/1 tensor. We write this tensor as
It is called the covariant derivative of 
.
Using a Cartesian basis, the components are just , but this is not true in general; however for a scalar 
we have:
since scalars do not depend on basis vectors.
Writing 
, we can find the transformation law for the components
of the Christoffel symbols .
This is just
We can calculate the covariant derivative of a one- form 
by using the fact that 
is a scalar for any vector
:
We have
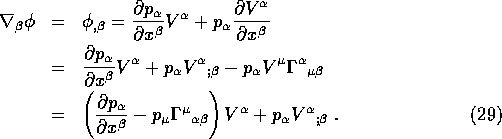
Since 
and are tensors, the term in
the parenthesis is a tensor with components:
We can extend this argument to show that
